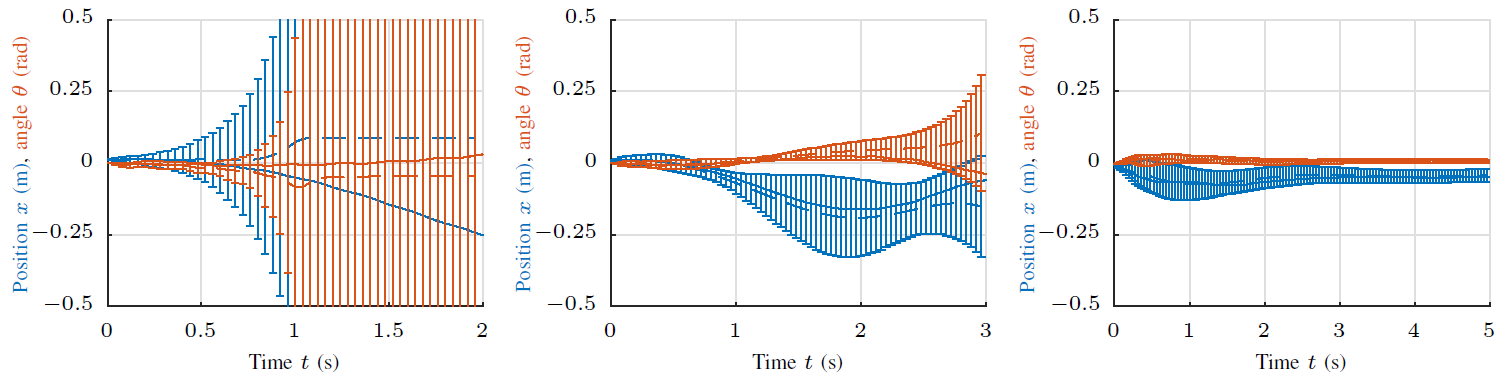
Figure 1: Visualization of the probabilistic, model-based optimization of multivariate PID controllers (iteration 1, 3, and 5). The predicted system behavior (dashed lines indicating mean prediction and errorbars indicate +/- 2 std) is visualized together with the observed behavior (solid lines). Both, pendulum angle (red) and end-effector position (blue) are shown for the inverted pendulum task.
Proportional, Integral and Derivative (PID) control architectures cover a significant portion of today’s industrial control applications. The PID control law for a Single-Input Single-Output (SISO) system is given by
u(t)=Kpe(t)+Ki∫Tτ=0e(τ)dt+Kd˙e(t)
with system input u, system output y, control gains Kp, Ki, Kd and error e=y–ydes This control law found widespread adoption thanks to its simplicity, the small number of open tuning parameters and the availability of simple tuning rules.
More complex systems, however, usually require the control of multiple coupled inputs given multi-dimensional system outputs. Manual tuning therefore quickly becomes tedious and simple heuristics are no longer applicable to coupled controllers.
In this project, we adapt general methods from model-based reinforcement learning (RL) to the specific PID architecture in particular for Multi-Input Multi-Output (MIMO) systems and possibly gain scheduled control designs. Based on the Probabilistic Inference for Learning Control (PILCO) framework, the finite horizon optimal control problem can be solved efficiently whilst incorporating model uncertainty in a fully probabilistic fashion.
In [ ], we demonstrate how to incorporate the PID controller in the probabilistic prediction and optimization step of PILCO. Therefore, arbitrary PID control structures can be optimized, whilst taking into account the full non-linear system dynamics and accounting for uncertainty caused by missing data or complex dynamics. Our proposed state augmentations enable efficient, gradient-based controller optimization.
We demonstrate iterative learning control without prior system knowledge on the robotic platform Apollo. Apollo, equipped with its 7 Degree-of-Freedom (DoF) arm, is learning to balance the inverted pendulum within 7 learning iterations (equivalent to around 100 sec of interaction time).
