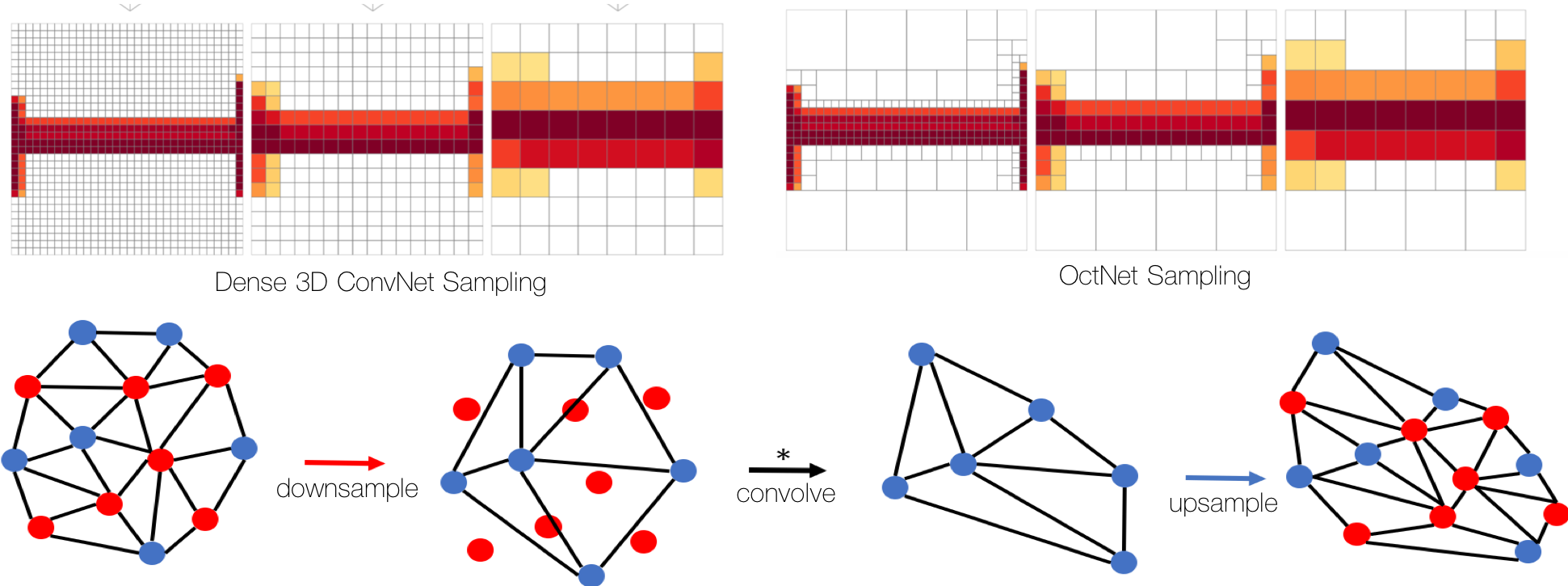
Top: OctNet represents 3D voxels using an oct-tree, which makes it computationally efficient for 3D convolutions. Bottom: Our Convolutional Mesh Autoencoder can efficiently perform convolutions and sampling directly on a mesh
Much of our work focuses on 3D models of objects and scenes. We would like to take advantage of current deep learning approaches in representing and reasoning about 3D. Unfortunately, the standard 2D convolutional models do not readily extend to 3D because they do not match well current 3D data structures. Consequently, we explore new representations and methods to enable 3D deep learning.
Another issue with applying deep learning to 3D data is that the amount of 3D data is limited relative to images. This means that, while 3D adds a dimension, the models must actually be smaller to prevent over fitting.
Voxels are a natural representation of 3D and are a straightforward generalization of 2D images. Convolutional operations are also simple to extend to voxels but are extremely inefficient in space and computation. Additionally, with voxel representations of shape, most voxels are empty and only a sparse set of voxels code the actual shape. To address these issues, we developed OctNet [ ], which extends convolutional models to the space-efficient octree representation. This focuses memory and computation on parts of the voxel space where shape is represented. OctNet means that deeper networks can be trained, which in turn improves the accuracy over a range of tasks.
Another common 3D shape representation in computer vision and graphics uses 3D meshes. It is common to learn low-dimensional linear models of 3D meshes using principal component analysis or higher-order tensor generalizations. To capture non-linear representations using deep learning, however, is a challenge as standard convolutional methods are not directly applicable to meshes of arbitrary topology. Consequently, we developed a Convolutional Mesh Autoencoder (CoMA) [ ] that generalizes CNNs to meshes by providing up- and down-sampling and convolutions using Chebyshev polynomials. This method performs 50% better than PCA models for modeling facial expressions in 3D. The low dimensional latent space learned by the CoMA can be used for sampling 3D meshes of diverse facial expressions.
Much work remains to learn representations of 3D shape, appearance, and material properties. Our ongoing work is exploring deep models of non-rigid and articulated objects.
