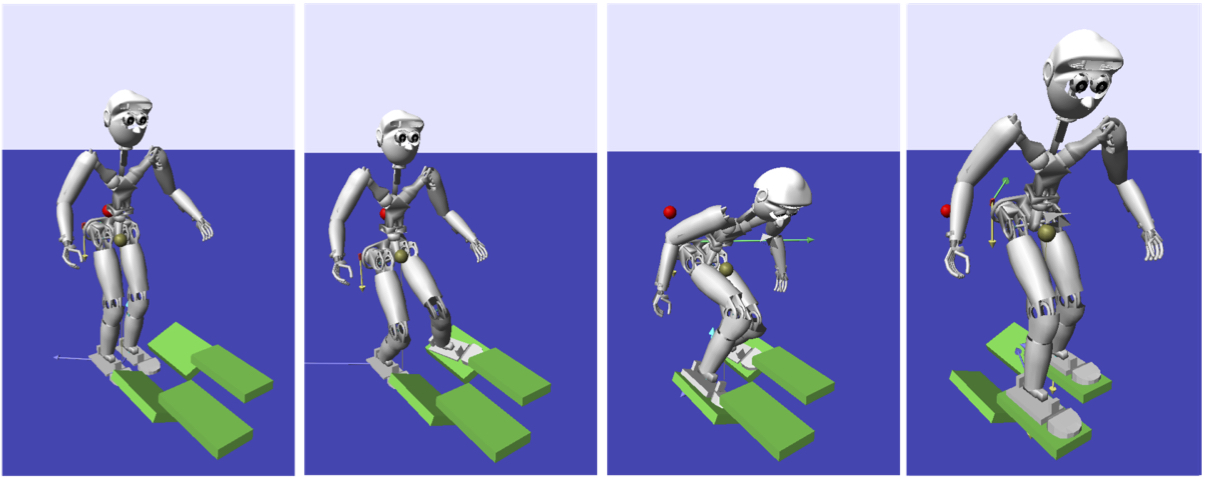
Our robot stepping on tilted stones that are increasing in height. Forces applied on the ground are planned and guaranteed to be admissible.
Planning dynamic behaviors for legged robots is a challenging task because the robot is subject to strong dynamic constraints due to its floating base (i.e. it can fall). It needs to take into account intermittent contacts with the environment and apply contact forces in order to move.
In this project, we address the problem of planning dynamic movements for legged robots that take into account the kino-dynamic constraints of the robot. We use optimal control techniques to find solutions that are dynamically feasible and to help synthesize feedback controllers to stabilize these plans. In particular, we are looking at the problem from three different points of view:
- Although legged robots typically consist of many joints, we believe that most of the dynamic behavior of walking or other dynamic tasks can be explained with an underlying (simpler) dynamics model. Thus, we would like to understand what is the level of complexity our models require in order to explain a dynamic behavior well, but at the same time serve in efficient planning and control algorithms.
- A common planning approach on robots with invertible dynamics (e.g. a manipulator) is to generate kinematic trajectories and then in a second step invert the dynamics to generate admissible torque trajectories. However, due to the Newton-Euler equations, a floating-base robot is under-actuated. We extend kinematic planning with trajectory generation on the under-actuated part and couple the two in a common optimization framework. [ ]
- In order to walk or climb, legged robots have to create and break contacts with the environment and apply forces at the contact support. Thus, an important part of our planning stage is finding good contact configurations leaving enough degrees of freedom to the robot for fulfilling its task.
